USB转串口线
#******USB转串口线的注意事项*******#
1. 由于Real6410的串口和PC机的一致,因此所购买的USB转串口线需要能先连接到
板子提供的串口线,然后再与板子连接.
2. 建议购买PL2303芯片的转接线,此芯片在2.6内核中有现成的驱动模块.
/lib/modules/`uname -r`/kernel/drivers/usb/serial/pl2303.ko
其他的芯片要看这个目录里面有没有驱动模块了.
3. 安装驱动模块.
一般在转接线接上后就能用了,如果不能就要手动加载驱动模块
$ modprobe pl2303
$ lsmod | grep pl2303
$ dmesg | tail
4. 测试.
将USB转串口线连接到PC上,再次用dmesg查看信息.
如果驱动正常工作,应该有类似如下字样:
pl2302 converter now attached to ttyUSB0
5. 使用.
$ minicom -s
在Serial port setup,将原来的设备名称ttyS0改为ttyUSB0
保存退出,重启minicom即可.
6. 补充:如果第4和第3步失败,那么设置开机驱动模块自动挂载.
在/etc/modprobe.conf中追加如下一行:
alias ttyUSB0 pl2303
#再次补充:
如果购买SD卡,不要买SDHC卡....
#再再次补充,看过S3C6410的手册后发现SDHC也是可以用的,只是要求块大小为512bytes.
具体参考:S3C6410 iROM的启动方式
网络配置
#***************网络配置****************#
1. tftp
# apt-get install tftp tftpd
# apt-get install inetutils-inetd
# mkdir /tftpboot
# vi /etc/inetd.conf
修改为: tftp dgram udp wait nobody /usr/sbin/tcpd /usr/sbin/in.tftpd /tftpboot
# /etc/init.d/inetutils-inetd reload
2. nfs
# apt-get install nfs-common nfs-kernel-server portmap
# mkdir /opt/nfsroot
# chmod 777 /nfsroot
# vi /etc/exports
添加一行: /opt/nfsroot *(rw,sync,no_subtree_check,subtree_check)
# /etc/init.d/nfs-kernel-server restart
第五章 计算及结果分析
5.1 模型计算调整
模型在上一章的设置后,基本可以进行迭代求解了。只是在迭代之前,还需对影响收敛的一些参数进行调整,以加速收敛的速度。
在控制方程以给定的方法离散化后,还必须对离散方程进行某种调整,并且对各未知量(速度、压力、温度)的求解顺序以及方式进行特殊处理。这些需要依赖流场计算方法(SIMPLE和SIMPLEC)来进行调整。
SIMPLE是英文Semi-Implicit Method for Pressure-Linked Equation的缩写,意为”求解压力耦合方程组的半隐式方法“。SIMPLE算法的基本思想可描述如下:对于给定的压力场(它可以是假定的,或是上次迭代计算所得的结果),求解离散形式的动量方程,得出速度场。因为压力场是假定的或不精确的,这样,由此得到的速度场一般不满足连续方程。因此,必须对给定的压力场加以修正。修正的原则是:与修正后的压力场相对应的速度场能满足这一迭代层次上的连续方程。据此原则,我们把由动量方程的离散形式所规定的压力与速度的关系代入连续方程的离散形式,从而得到压力修正方程,由压力修正方程得出压力修正值。接着,根据修正后的压力场,求得新的速度场。然后检查速度场是否收敛。若不收敛,用修正后的压力值作为给定的压力场,开始下一层的计算,如此反复,直到获得收敛的解。
SIMPLEC是SIMPLE的改进算法之一,由Van Doormal和Raithby提出。其稳定性较好,在计算中可以将亚松驰因子适当放大,特别是在层流计算时,如果没有在计算中使用辐射模型等辅助方程,用SIMPLEC可以大大加速计算速度。因此,本模型在层流计算时选用SIMPLEC算法,在湍流时选用SIMPLE算法。
因为Fluent中解的方程为非线性,所以有必要对变量[tex]\phi[/tex]的变化进行控制。通常的方法便是调整亚松驰因子,以减小在迭代过程中[tex]\phi[/tex]的变化。一般情况下,一个单元(cell)中的新值[tex]\phi[/tex]依赖于上一个旧值[tex]\phi_{old}[/tex]。亚松驰因子[tex]\alpha[/tex]因此定义为:
[tex]\phi=\phi_{old}+\alpha \Delta \phi[/tex] (5-1)
由此公式可见,调节亚松驰因子直接影响着计算收敛的速度。在计算过程中,先以默认亚松驰因子迭代,当残差曲线下降过于缓慢时可适当减小亚松驰因子以加速收敛速度。
初始化时迭代计算前最重要的一步,初始化数值是否恰当是影响计算收敛的最重要因素之一。本模型经过不断的摸索尝试,总结出恰当的初始化方式和数值。全局初始化以压力出口为参考,压力值设为1000Pa。待全局初始化完毕,再对其进行适当的修改。在Path面板中,设置Fluid zone的压力为1000Pa,Z方向的速度值为速度入口的值,温度为300K。
收敛条件以默认值为准,即残差值分别为:Continuity 1e-3;X-Velocity 1e-3;Y-Velocity 1e-3;Z-Velocity 1e-3;k 1e-3;epsilon 1e-3;Energy 1e-6。绘制残差曲线以监视计算收敛情况。
另外,在进行迭代计算前还需建立等值面(ISO-Surface)用以生成等值线图和矢量图。以[tex]y=3mm[/tex]建立Surface Zone,即板翅式换热器模型在其高度一半处沿流动方向的一个分割面。
计算残差图如下:
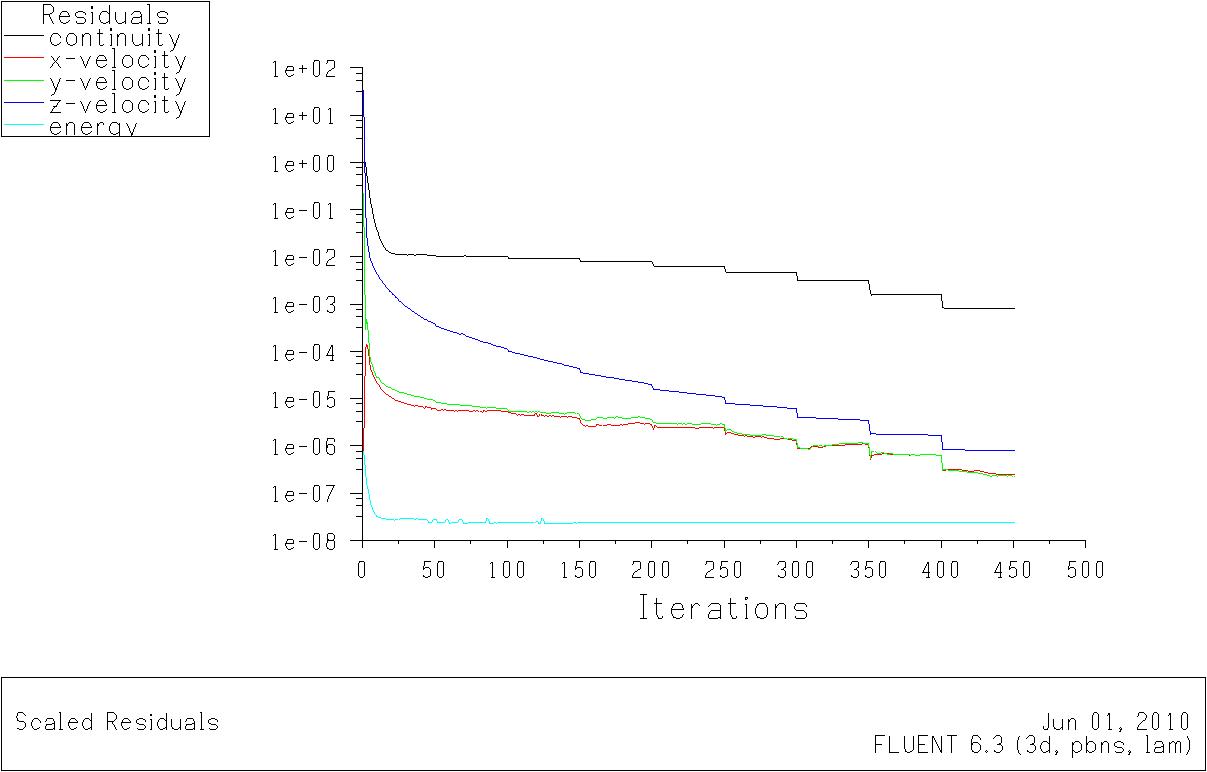
图 5-1 模型一在Re=500时的残差图
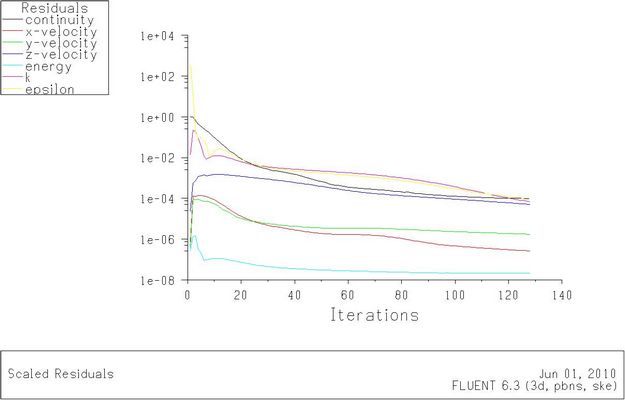
图 5-2 模型一在Re=9500时的残差图
5.2 计算结果分析
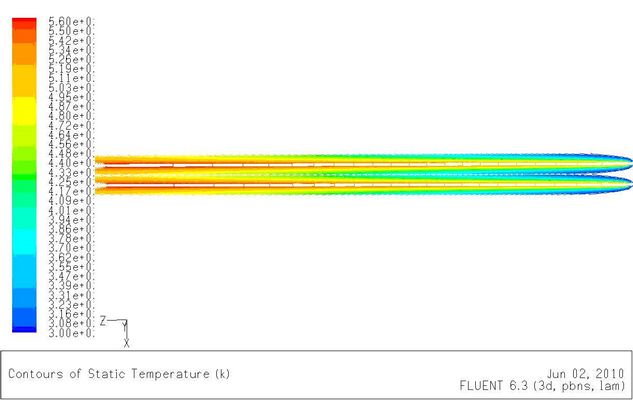
当流体从空间进入管道时,流动的边界层会有一个从零到汇合于流道中心线的过程。相同的,热边界层也如此。当热边界层汇合于中心线后,换热已经充分发展,此后的换热强度将不再保持不变。如图5-3所示。
图5-3(a)Re=500时温度分布图
图5-3(b)Re=9500时温度分布
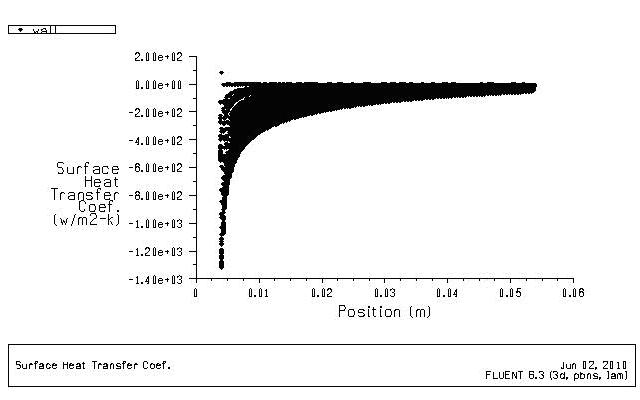
入口段的热边界层较薄,局部换热系数比充分发展段的高,且沿流动方向逐渐降低。如图5-4 可以反映这点。
图 5-4 局部换热系数沿流动方向的变化
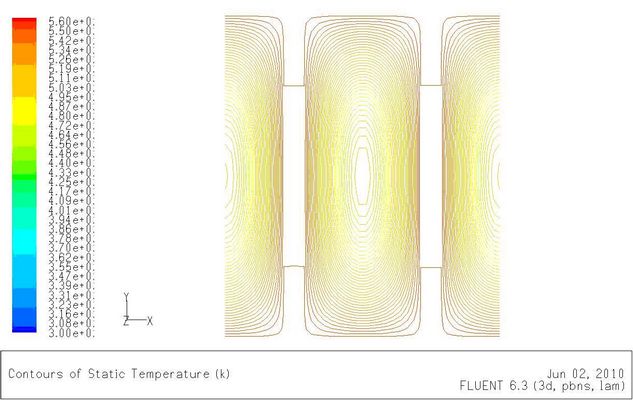
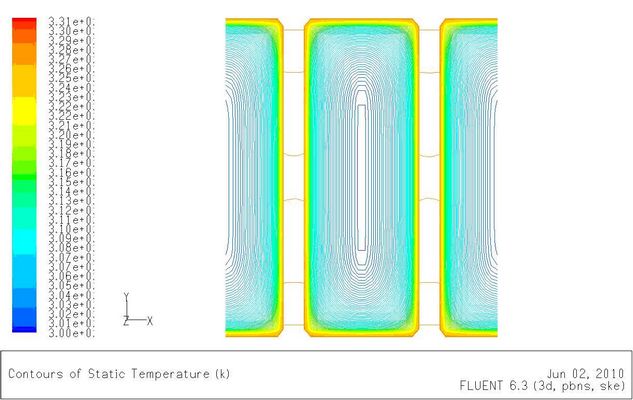
流体在热边界层内的换热剧烈,温度从壁面到热边界层外迅速降低。此后,温度与流体的主流温度变化微小,近似呈恒温状。平直型的板翅式换热器,其流道相当于圆管。热边界层的发展也类似于圆管。图5-5(a)是Re=500时垂直于流动方向40毫米处截面的温度分布,图5-5(b)是Re=9500时垂直于流动方向40毫米处处截面的温度分布。比较两图可以发现在高雷诺数时热边界层发展较快,在相同距离处其厚度较低雷诺数要大。因此可以推断,平直型的板翅式换热器在高雷诺数时其换热性能低于低雷诺数。
图 5-5(a)Re=500时,
图5-5(b)Re=9500时,
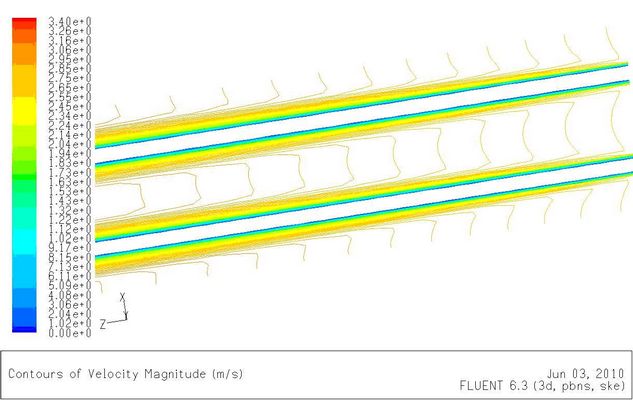
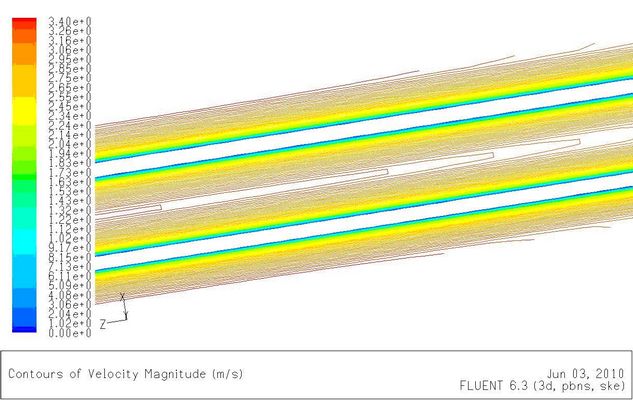
如图5-6(a),在z=0处开始,流体在壁面上被滞止,形成边界层。边界层外即流道中心,仍保持较为均匀的流速,为核心流。由壁面不滑移条件引起壁面附近的流速降低,为满足质量守恒定律,核心流流速增大,速度等值线由平坦逐渐变为凸出。随着边界层厚度不断增长,核心流不断加速,直至四周边界层相遇,如图5-6(b)。整个流道被边界层流动充满,此后速度等值线不再变化。
图5-6(a)入口处速度分布
图5-6(b)流道中段速度分布图
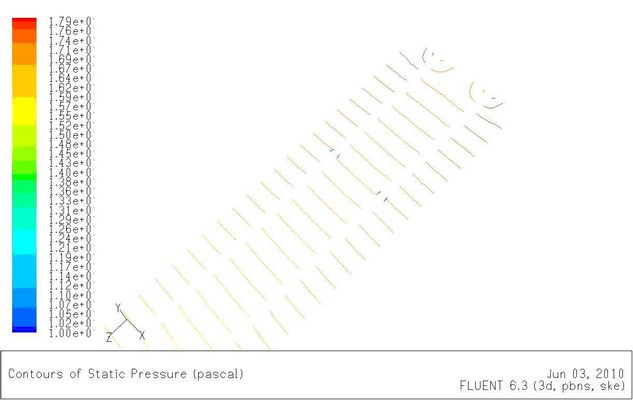
观察图5-7入口处压力等值线,可以发现在流道入口处存在较大压降。此处的压降可以解释为两点:一是如图5-6(a)所示,是由于均流加速成充分发展流动引起的压降;二是入口段壁面速度等值线陡峭,壁面切应力大于充分发展段的壁面切应力,为克服这不负阻力差值所需要的压降。
图5-7入口压力分布图
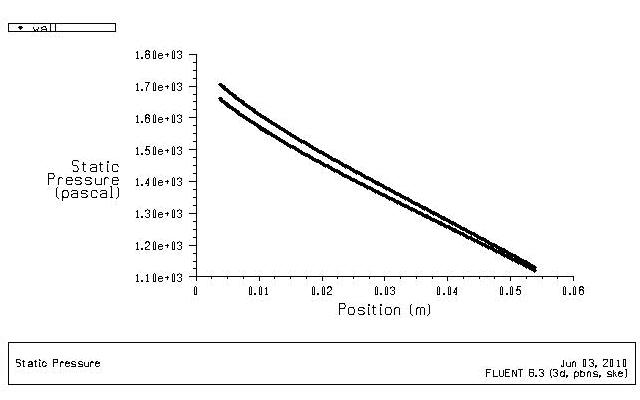
观察图5-8摩擦因子沿流动方向的数值变化,在入口处由于入口效应的影响其摩擦因子较大。随后其数值逐渐降低,是由于随着流体向充分流动的发展,流体趋于稳定。但随后摩擦因子略微增加,是因为随着流速的增加流体的粘性底层逐渐变薄,流动由“水力光滑区”向“粗糙区”发展。管壁的粗糙度影响逐渐显现,摩擦因子增大。平直型翅片的压强降落平滑,压降数值不高,如图5-9.
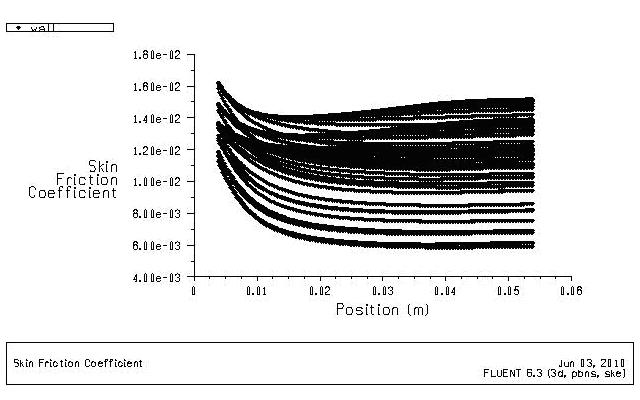
图5-8 摩擦因子沿流动方向的数值分布
图5-9压强沿流动方向的降落
5.2.3 j,f因子综合分析
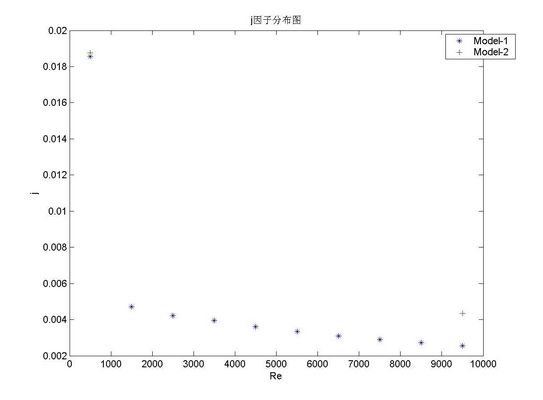
由j因子分布图可知,平直型翅片在高雷诺数时换热效率差,所以其应该用于低雷诺数的范畴。相同雷诺数下模型二j因子与模型型一的比较可以看出,翅片高度对j因子的影响。在较高的翅片高度时,其换热效率较高。但由于翅片属于二次表面,其传热效率低于一次传热表面,所以可以预见在更大的翅片高度时相同雷诺数下其j因子反而会减小。这是由翅片的特性决定的。
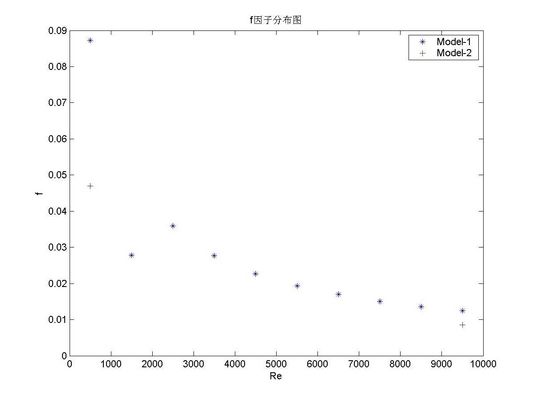
由f因子的分布图可知,平直型翅片是一种适合应用于较低压降的翅片形式。如粘度较高的液体,或夹杂着固体颗粒的流体。这是由其简单的流道结构决定的。在相同雷诺数下模型二与模型一的对比可以看出,在较大的翅片高度下摩擦因子较小。这是因为模型二与模型一翅片宽度相近,在较大的翅片高下其最小自由流通面积较大,摩擦阻力减小。
图5-10 j因子分布图
图5
由于计算资源的限制,未能得到更多的模拟数据。但从现有的数据来看,猜测平直型翅片的j,f因子除与雷诺数相关外,还与翅片高度与宽度相关。但具体说来,应该是与翅片高与宽的比值有很大的关联。在某一雷诺数下,应该存在一个恰当的高宽比,使j,f因子达到最大,即整体效率最高。
第四章 数值模型的建立
4.1 计算流体动力学简介
计算流体动力学(Computatonal Fluid Dynamics,简称CFD)是通过计算机数值计算和图像显示,对包含有流体流动和热传导等相关物理现象的系统所作的分析。CFD的基本思想可以归结为:把原来在时间域及空间域上连续的物理量的场,如速度场和压力场,用一系列有限个离散点上的变量值的集合来代替,通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组,然后求解代数方程组获得场变量的近似值。(周雪漪 计算水力学 清华大学出版社 1995 陶文铨 数值传热学(第二版)西安交通大学出版社 2001 郭鸿志 传输过程数值模拟 冶金工业出版社 1998)
采用CFD的方法对流体流动进行数值模拟,通常包括以下步骤:
(1) 建立反映工程问题或物理问题本质的数学模型。具体说来就是要建立反映问题各个量之间关系的微分方程及相应的定解条件,这是数值模拟的出发点。没有正确完善的数学模型,数值模拟就毫无意义。流体的基本控制方程通常包括质量守恒方程、动量守恒方程、能量守恒方程,以及这些方程相应的定解条件。
(2)寻求高效率、高准确度的计算方法,即建立针对控制方程的数值离散化方法,如有限差分法、有限元法、有限体积法等。这里的计算方法不仅包括微分方程的离散化方法及求解方法,还包括贴体坐标的建立,边界条件的处理等。这些内容,可以说是CFD的核心。
(3)编制程序和进行计算。这部分工作包括计算网格划分、初始化和边界条件的输入、控制参数的设定等。这是整个工作中花时间最多的部分。由于求解的问题比较复杂,比如Navier-Stokes方程就是一个十分复杂的非线性方程,数值求解方法在理论上不是绝对完善的,所以需要通过实验加以验证。正式从这个意义上讲,数值模拟又叫数值试验。
(4)显示计算结果。计算结果一般通过图表等方式显示,这对检查和判断分析质量和结果有重要参考意义。
以下将以以上4点为纲领,详细叙述模型的建立和计算过程。
本文使用商业CFD软件Fluent及其前置软件Gambit来进行模拟,使用压力基解算器求解。压力基求法原称为分离求解方法,即分别求解各个控制方程的方法。由于控制方程是非线性的,因此求解必须经过多次迭代才能获得收敛解。图4-1为求解流程图,其过程可概述如下:
(1)流场变量更新。在第一次计算时,变量由初始化过程更新。在随后的计算中,没迭代一部既得到一个更新的解。
(2)用当前压强和质量通量的值求解动量方程,以得到新的速度场。
(3)因为(2)中得到的速度场的数值解无法完全满足连续方程,于是再求解压强修正方程。压强修正方程是由连续方程导出的泊松型方程,求解这个方程可以得到对压强场、速度场和质量通量的修正,进而使连续方程得到满足。
(4)利用前面求出的解,求解湍流方程、能量方程和组元方程。
(5)在多项流计算中那个如果考虑相间干扰,则需要通过求解弥散相轨迹计算得到连续相方程中的源项解。
(6)检验收敛条件是否满足。如果收敛条件满足,则停止计算。如果计算没有收敛,则继续迭代过程。
图 4-1
4.2 流体的控制方程及其离散化
设[tex]\phi[/tex]为流体系统在[tex] t [/tex]时刻所具有的某种物理量,[tex]\phi_{p}[/tex]表示单位质量流体所具有的这种物理量。
由此推导出输运方程为:
[tex]\frac{d\phi}{dt}=\frac{\partial}{\partial t} \int \limits_{CV}\phi_{p} \rho d V+\int \limits_{CS}\phi_{p} \rho u_{n} dA[/tex] (4-1)
其中[tex]u_{n}[/tex]为速度在微元面法线方向的投影。该式表明,流体某一物理量时间的全变化率等于控制体内这种物理量的时间变化率与经过控制面的这种物理量的净通量之和。
单位质量的流体的质量[tex]\phi_{p}=1[/tex],质量为[tex]\phi=\int \limits_{V}\rho d V=m[/tex]因为质量守恒,所以有:
[tex]\frac{d \phi}{d t}=\frac{d m}{d t}=0[/tex]
由(4-1)式可得:
[tex]\frac{\partial}{\partial t}\int \limits_{CV}\rho d V+\int\limits_{CS}\rho u_{n} d A=0[/tex] (4-2)
此即是连续方程的积分形式,其微分形式为:
[tex]\frac{\partial \rho}{\partial t}+\nabla \cdot(\mathbf{\rho u})=0[/tex] (4-3)
在直角坐标系中表示为:
[tex]\frac{\partial \rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}=0[/tex] (4-4)
单位质量的流体动量为[tex]\phi_{p}=u[/tex],流体系统动量为[tex]p=\int \limits_{V}\rho \mathbf{u} d V[/tex],由(4-1)式得:
[tex]\frac{d}{d t}\int \limits_{V}\mathbf{u}\rho d V=\frac{\partial}{\partial t}\int \limits_{CV}\mathbf{u}\rho d V+\int \limits_{CS}\mathbf{u}\rho u_{n}d A[/tex] (4-5)
根据质点系动量定理,流体系统动量的时间变化率等于作用在系统上的外力之和。作用在流体流体微元上的外力有质量力和表面力之分。定义[tex]f[/tex]为作用在单位质量流体上的质量力分布函数,定义[tex]p_{n}[/tex]为作用在单位质量流体上的表面力分布函数。那么运动方程的完整积分表述方式为:
[tex]\frac{\partial}{\partial t}\int \limits_{CV}\mathbf{u}\rho d V+\int \limits_{CS}\mathbf{u}\rho u_{n} d A=\int \limits_{CV}f \rho d V+\int \limits_{CS}p_{n} d A[/tex] (4-6)
[tex]\because \quad \frac{d}{d t}\int \limits_{V}\mathbf{u}\rho d V=\int \limits_{V}\rho \frac{d \mathbf{u}}{d t}d V[/tex]
又根据奥高定理:
[tex]\int \limits_{CS}p_{n} d A=\int \limits_{CS}\mathbf{n} \cdot P d A=\int \limits_{CV}\nabla \mathbf{P} d V[/tex]
于是式(4-6)变为:
[tex]\int \limits_{CV}(\rho \frac{d \mathbf{u}}{d t}-\rho \mathbf{f}-\nabla \mathbf{P}) d V=0[/tex]
[tex]\therefore \quad \rho\frac{d \mathbf{u}}{d t}=\rho\mathbf{f}+\nabla\mathbf{P}[/tex] (4-7)
此即是运动方程的微分形式
在直角坐标系中,变为:
[tex]\rho(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z})=\rho f_{x}+\frac{\partial p_{xx}}{\partial x}+\frac{\partial p_{xy}}{\partial y}+\frac{\partial p_{xz}}{\partial z}[/tex] (4-8a)
[tex]\rho(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z})=\rho f_{y}+\frac{\partial p_{yx}}{\partial x}+\frac{\partial p_{yy}}{\partial y}+\frac{\partial p_{yz}}{\partial z}[/tex] (4-8b)
[tex]\rho(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z})=\rho f_{z}+\frac{\partial p_{zx}}{\partial x}+\frac{\partial p_{zy}}{\partial y}+\frac{\partial p_{zz}}{\partial z}[/tex] (4-8c)
由本构方程:
[tex]p_{xx}=-p-\frac{2}{3}\mu \nabla \mathbf{u}+2\mu\frac{\partial u}{\partial x}[/tex]
[tex]p_{yy}=-p-\frac{2}{3}\mu \nabla \mathbf{u}+2\mu\frac{\partial v}{\partial y}[/tex]
[tex]p_{zz}=-p-\frac{2}{3}\mu \nabla \mathbf{u}+2\mu\frac{\partial w}{\partial z}[/tex]
[tex]p_{xy}=p_{yx}=\mu(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})[/tex]
[tex]p_{zx}=p_{xz}=\mu(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})[/tex]
[tex]p_{yz}=p_{zy}=\mu(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})[/tex]
代入式(4-8)得到N-S方程:
[tex]\rho \frac{Du}{Dt}\!=\!\rho f_{x}\!-\!\frac{\partial p}{\partial x}\!+\!\frac{\partial}{\partial x}[\mu(2\frac{\partial u}{\partial x}\!-\!\frac{2}{3}\nabla \mathbf{u})]\!+\!\frac{\partial}{\partial y}[\mu(\frac{\partial v}{\partial x}\!+\!\frac{\partial u}{\partial y})]\!+\!\frac{\partial}{\partial z}[\mu(\frac{\partial u}{\partial z}\!+\!\frac{\partial w}{\partial x})][/tex] (4-9a)
[tex]\rho \frac{Dv}{Dt}=\rho f_{y}-\frac{\partial p}{\partial y}+\frac{\partial}{\partial x}[\mu(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y})]+\frac{\partial}{\partial y}[\mu(2\frac{\partial v}{\partial y}-\frac{2}{3}\nabla \mathbf{u})]+\frac{\partial}{\partial z}[\mu(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z})][/tex] (4-9b)
[tex]\rho \frac{Dw}{Dt}=\rho f_{z}-\frac{\partial p}{\partial z}+\frac{\partial}{\partial x}[\mu(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})]+\frac{\partial}{\partial z}[\mu(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z})]+\frac{\partial}{\partial z}[\mu(2\frac{\partial w}{\partial z}-\frac{2}{3}\nabla \mathbf{u})][/tex] (4-9c)
当流体为均质不可压缩常粘度时,N-S方程简化为:
[tex]\rho(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z})=\rho f_{x}-\frac{\partial p}{\partial x}+\mu(\frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}}+\frac{\partial^{2}u}{\partial z^{2}})[/tex] (4-10a)
[tex]\rho(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z})=\rho f_{y}-\frac{\partial p}{\partial y}+\mu(\frac{\partial^{2}v}{\partial x^{2}}+\frac{\partial^{2}v}{\partial y^{2}}+\frac{\partial^{2}v}{\partial z^{2}})[/tex] (4-10b)
[tex]\rho(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z})=\rho f_{z}-\frac{\partial p}{\partial z}+\mu(\frac{\partial^{2}w}{\partial x^{2}}+\frac{\partial^{2}w}{\partial y^{2}}+\frac{\partial^{2}w}{\partial z^{2}})[/tex] (4-10c)
单位质量的流体的能量为[tex] \phi_{p}=e+u^{2}/2[/tex],其中[tex]e[/tex]为单位质量流体的热力学能。则[tex]\phi=\int \limits_{V}(e+u^{2}/2)\rho d V[/tex],由(4-1)式得:
[tex]\frac{d}{dt}\int \limits_{V}(e+u^{2}/2)\rho d V=\frac{d}{dt}\int \limits_{CV}(e+u^{2}/2)\rho d V+\int \limits_{CS}(e+u^{2}/2)\rho v_{n}d V[/tex] (4-11)
根据能量守恒和转换定律,流体系统中能量的时间全变化率等于作用在系统上的质量力和表面力所作的功率和与外界换热率之和。则得:
[tex]\frac{d}{dt}\int \limits_{V}(e+u^{2}/2)\rho d V=\int \limits_{V}f \rho \mathbf{u} d V+\int \limits_{CA}p_{n} \mathbf{u} d A+Q[/tex] (4-12)
则能量守恒方程积分形式为:
[tex]\frac{d}{dt}\int \limits_{CV}(e+u^{2}/2)\rho d V+\int \limits_{CS}(e+u^{2}/2)\rho v_{n}d V=\int \limits_{V}f \rho \mathbf{u} d V+\int \limits_{CA}p_{n} \mathbf{u} d A+Q[/tex] (4-13)
其微分形式为:
[tex]\frac{\partial \rho T}{\partial t}+\frac{\partial \rho u T}{\partial x}+\frac{\partial \rho v T}{\partial y}+\frac{\partial \rho w T}{\partial z}=\frac{\partial}{\partial x}(\frac{\lambda}{c_{p}}\frac{\partial T}{\partial x})+\frac{\partial}{\partial y}(\frac{\lambda}{c_{p}}\frac{\partial T}{\partial y})+\frac{\partial}{\partial z}(\frac{\lambda}{c_{p}}\frac{\partial T}{\partial z})+Q[/tex] (4-14)
对于不可压缩,常物性无内热源可简化为:
[tex]\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}=\frac{\lambda}{\rho c_{p}}(\frac{\partial^{2}T}{\partial x^{2}})+\frac{\partial^{2}T}{\partial y^{2}}+\frac{\partial^{2}T}{\partial z^{2}}[/tex] (4-15)
比较基本的控制方程,可以看出,尽管这些方程中因变量各不相同,但它们均反映了单位时间单位体积内物理量的守恒性质。用 [tex]\phi[/tex]表示通用变量,则上述控制方程可以表示成以下通用形式:
[tex]\int \limits_{V}\frac{\partial \rho \phi}{\partial t}dV+\oint \rho \phi \mathbf{u}\cdot d\mathbf{A}=\oint \Gamma_{\phi}\nabla \phi \cdot d\mathbf{A}+\int \limits_{V}S_{\phi}dV[/tex] (4-16)
其中[tex]\Gamma_{\phi}[/tex]是变量[tex]\phi[/tex]的扩散系数
[tex]S_{\phi}[/tex]是[tex]\phi[/tex]的单位体积源项
转化为微分形式为:
[tex]\frac{\partial(\rho \phi)}{\partial t}+\nabla \cdot (\rho \mathbf{u}\phi)=\nabla \cdot (\Gamma_{\phi}\nabla \phi)+S_{\phi}[/tex] (4-17)
式中从左到右依次代表瞬态项、对流项、扩散项和源项。
对反映物理问题的控制方程离散化是数值模拟里核心的 步骤,离散化方式的选择决定着计算的稳定性和精度。目前成熟和应用较多的离散化方式有:有限差分法(Finite Difference Method)、有限元法(Finite Element Method)和有限体积法(Finite Volume Method)。
有限体积法的基本思路是:将计算区域划分为网格,并使每个网格点周围有一个互不重复的控制体积;将待解的微分方程对每一个控制体积积分,从而得到一组离散方程。其中的未知数是网格点上的因变量[tex]\phi[/tex]。为了求出控制体积的积分,必须假定[tex]\phi[/tex]值在网格点之间的变化规律。在有限体积法的网格中,计算节点(node)被看成是控制体积(cell)的代表。在离散化过程中,将一个控制体积上的物理量定义并储存在该节点处。在有限体积法中,计算节点的值即因变量[tex]\phi[/tex]处于控制体积的中心,有异于网格交点。其数值的确定方式和在节点间的数值传递(变化)方式即是离散化方式。
Fluent对于时间上的偏导数,有一阶和二阶的显式或隐式格式可选。由于本文讨论的问题为定常流动,因此控制方程中没有瞬态项。对于空间上的离散方式即对对流项和扩散项的[tex]\phi[/tex]值的离散,通常有一阶迎风、二阶迎风、中心差分和QUICK等格式。一阶迎风格式将控制体积界面上的未知量[tex]\phi_{f}[/tex]恒取上游的计算节点的值,即:
[tex]\phi_{f}=\phi[/tex]
而二阶迎风格式在一阶迎风的基础上考虑了物理量在节点间分布曲线的曲率影响,其表示为:
[tex]\phi_{f}=\phi+\nabla \phi \cdot \mathbf{r}[/tex]
其中[tex]\phi \quad \nabla \phi[/tex]分别为计算节点的值和其在上游节点的梯度
[tex]\mathbf{r}[/tex]为上游节点质心道界面质心的方向向量
中心差分格式计算控制体积界面上的值[tex]\phi_{f}[/tex]为:
[tex]\phi_{f}=\frac{1}{2}(\phi_{0}+\phi_{1})+\frac{1}{2}(\nabla \phi_{0}\cdot \mathbf{r_{0}}+\nabla \phi_{1}\cdot \mathbf{r_{1}})[/tex]
其中[tex]\phi_{0} \quad \phi_{1}[/tex]指共面于[tex]f[/tex]的控制体的计算节点值
本文所建立的模型流动方向与网格方向基本一致,且为结构化网格,因此选用一阶迎风格式。一阶迎风格式具有稳定性高,计算速度快的优点。对于[tex]\nabla \phi[/tex]的离散化,在Fluent中使用Green-Gauss理论,分别有Cell-Based和Node-Based两种方法。对于控制体中心[tex]c0[/tex]的值[tex]\phi[/tex],其梯度的离散化形式为:
[tex](\nabla \phi)_{c0}=\frac{1}{V}\sum \limits_{f}\overline{\phi_{f}}\mathbf{A_{f}}[/tex] (4-18)
Cell-Based方法:
[tex]\overline{\phi_{f}}=\frac{\phi_{c0}+\phi_{c1}}{2}[/tex] (4-19)
Node-Based方法:
[tex]\overline{\phi_{f}}=\frac{1}{N_{f}}\sum \limits_{n}^{N_{f}}\overline{\phi_{n}}[/tex] (4-20)
其中[tex]N_{f}[/tex]——界面上的节点数
[tex]\overline{\phi_{n}}[/tex]——包围节点的单元的值的加权平均
Node-Based方法比默认的Cell-Based方法精度更高,因此本模型选用Node-Based方法计算[tex]\nabla \phi[/tex]。
4.3 几何模型的建立及网格化
本文用Gambit建立两个平直型翅片的模型,其尺寸参数分别为:
模型一 模型二
水力直径mm 2.45 2.79
翅片间距mm 2.0 2.1
翅片厚度mm 0.3 0.3
翅片高度mm 4.7 6.5
隔板厚度mm 0.5 0.5
流动长度mm 50 50
由于翅片很薄,其与板片接触部分以钎焊连接,换热量少。为了简化模型,减少网格数量节约计算资源将此部分去除。此外,参考1947年美国海军研究署的实验装置,取板翅式换热器一个完整流道和其相邻的两个流道的一半,建立模型结构如图4-2。
图 4-2
图中1-2-3部分为流体区域,上下板片及翅片被分割为12部分。注意在Gambit中对体的切割有连接(connected)和非连接(unconnected)之分,非连接的体在其交接面出产生连个重叠的面,在载入Fluent时默认为两个壁面(wall)。如果两个壁面间有参数的传递,比如流体/固体内部或流固耦合处。则这种设置将阻断参数的传递,使其彼此成为孤立的体。若要使其之间有参数的传递,即使其网格结构不同或属于流固两种区域,则需要使其连接或分别定义为interface边界条件。interface边界条件为不同网格结构的区域提供了一种插值的参数传递方式,然而其设置繁杂,会增加计算量且存在一定误差。此处体的分割均为连接。即两个分割的体公用一面,在载入Fluent时会自动生成wall和wall.shadow两个壁面。其中一个为虚拟壁面,Fluent自动耦合两壁面间参数。
由于平直型翅片几何结构较为规整,因此使用六边形的网格单元以map的方式分别网格化图 4-2中的各区域。考虑到网格密度对计算精度的影响,先行对各待网格化的区域在流动方向上的面和流体入口面的边网格化,设置合适的网格数量。得到整体网格如下图 4-3
图 4-3
为了减少入口效应和出口效应,在流体的进口处和出口处分别建立延长段。进口延长段长度为进口水力直径的1.5倍,出口延长段长度为出口水力直径的5倍,如上图。
4.4 解的设置
4.4.1 边界条件
此模型考虑到计算资源有限,采用压力基隐式求解方式。因此将流体近似认为不可压缩流体,密度取为常数。因为速度入口条件应用于不可压缩流体,且比质量流量入口条件稳定,因此流体入口定义为速度入口边界条件。入口流体的温度保持为300K,以考察各模型对流体的加热情况。速度方向设置为垂直于边界(Normal to Boundary),所以忽略了导流片对流动分配的影响,近似认为入口流动是均匀的。
模型一预期取得十个实验数据点,雷诺数从500~9500以1000递增。模型二取雷诺数500和9500两个数据点与模型一对比。模型一速度入口的速度值与雷诺数对应为:
速度m/s 雷诺数
1.4 500
4.2 1500
6.95 2500
9.7 3500
12.5 4500
15.3 5500
18 6500
20.87 7500
23.65 8500
26.4 9500
模型二速度与雷诺数对应为:
速度m/s 雷诺数
2.2 500
39.36 9500
对于雷诺数由2500~9500的情形,虽然实际上流体处于过度流动阶段。然而在模拟中使用湍流模型,调整湍流强度来模拟其流动状况。界面上的湍流强度定义为:
[tex]I=\frac{\sqrt{u^{'2}+v^{'2}+w^{'2}}}{u_{avg}}[/tex] (4-21)
其中[tex]u^{'},v^{'},w^{'}[/tex]是速度脉动量,[tex]u_{avg}[/tex]是平均速度。
湍流强度小于1%时,可以认为湍流强度是比较低的,而在湍流强度大于10%时,则可以认为湍流强度是比较高的。内流问题的湍流强度取决于上游的流动状态。如果上游是没有充分发展的未受扰动的流动,则进口处可以使用低湍流强度。如果上流是充分发展的湍流,则进口处湍流强度可以达到几个百分点。鉴于此,考虑到本模型的实际情况,选用较小的湍流强度。其数值在1%到10%浮动,以水力直径为特征长度。
压力出口边界条件指定出口边界处的静压,而静压值仅在流场为亚音速时使用。如果在出口边界上流场达到超音速,则边界上的压强将从流场内部通过插值得到。其他流场变量均从流场内部插值获得。定义压力出口的静压值均为1000Pa(表压),无回流,回流温度均为零。
定义板片的上下两个面为定热流密度(热通量)的壁面,热流密度均设置为[tex]20000W/m^{2}[/tex]。定义模型的左右各个面为对称边界条件。其余的面均定义为绝热壁面。
4.4.2 物理材质的物性参数定义
对于Fluent中的物理材质,还需根据本模型的具体情况进行调整。
空气的密度设置为常数,其数值为[tex]1.5 kg/m^{3}[/tex]。定压比热容以温度的多项式计算,设置为式(2-24)。导热系数以运动理论计算,设置为式(2-22)。运动粘度系数以Sutherland三系数公式计算,系数取默认值。
固体材质为铝,其密度、比热容和导热系数均认为常数。其值分别设置为[tex]\rho=2770ka/m^{3} \quad c_{p}=963J/(kg\cdot K) \quad \lambda=175W/(m\cdot K)[/tex]。
4.4.3 湍流模型及壁面函数定义
本文模型选用Standard[tex]k-\epsilon[/tex]湍流模型,标准的[tex]k-\epsilon[/tex]模型通过解两个独立的输运方程来求取湍动粘度[tex]\mu_{t}]/tex]和湍流尺度[tex]l[/tex]。湍动能[tex]k[/tex]和湍动耗散率[tex]\epsilon[/tex]的输运方程分别为:
[tex]\frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_{i}}(\rho k u_{i})=\frac{\partial}{\partial x_{j}}[(\mu+\frac{\mu_{t}}{\sigma_{k}})\frac{\partial k}{\partial x_{j}}]+G_{k}+G_{b}-\rho \epsilon-Y_{M}+S_{k}[/tex] (4-22a)
[tex]\frac{\partial}{\partial t}(\rho \epsilon)+\frac{\partial}{\partial x_{i}}(\rho \epsilon u_{i})=\frac{\partial}{\partial x_{j}}[(\mu+\frac{\mu_{t}}{\sigma_{\epsilon}})\frac{\partial \epsilon}{\partial x_{j}}]+C_{1\epsilon}\frac{\epsilon}{k}(G_{k}+C_{3\epsilon}G_{b})-C_{2\epsilon}\rho \frac{\epsilon^{2}}{k}+S_{\epsilon}[/tex] (4-22b)
其中:[tex]k[/tex]——湍动能
[tex]\epsilon[/tex]——湍动耗散率
[tex]G_{k}[/tex]——平均速度梯度对湍动能的影响系数
[tex]G_{k}=-\rho \overline{u_{i}^{'}u_{j}^{'}}\frac{\partial u_{i}}{\partial x_{i}}[/tex]
根据Boussinesq 假设:
[tex]G_{k}=\mu_{t}S^{2}[/tex] (4-23)
其中[tex]S[/tex]为平均应力张量系数
[tex]G_{b}[/tex]——浮力(弹性力)对湍动能的影响系数
[tex]G_{b}=\beta g_{i}\frac{\mu_{t}}{P_{rt}}\frac{\partial T}{\partial x_{i}}[/tex] (4-24)
其中[tex]P_{rt}[/tex]——湍动能的普朗特数,默认设置为0.85
[tex]g_{i}[/tex]——重力加速度在[tex]i[/tex]方向的分量
[tex]\beta[/tex]——热力扩散系数
[tex]\beta=-\frac{1}{\rho}(\frac{\partial \rho}{\partial T})_{p}[/tex] (4-25)
[tex]Y_{M}[/tex]——流体的可压缩性对湍动耗散率的影响系数
[tex]Y_{M}=2\rho \epsilon M_{t}^{2}[/tex]
其中[tex]M_{t}[/tex]——湍流马赫数
[tex]M_{t}=\sqrt{\frac{k}{s}}[/tex] (4-26)
其中[tex]s[/tex]——当地声速
[tex]C_{1\epsilon},C_{2\epsilon},C_{3\epsilon}[/tex]——常数,默认设置值为1.44,1.92。
[tex]\sigma_{k},\sigma_{\epsilon}[/tex]——分别是湍动能和湍动耗散率的普朗特数,默认设置值为1.0,1.3。
[tex]S_{k},S_{\epsilon}[/tex]——用户自定义源项。
[tex]\mu_{t}[/tex]——湍流粘度
[tex]\mu_{t}=\rho C_{\mu} \frac{k^{2}}{\epsilon}[/tex] (4-27)
其中[tex]C_{\mu}[/tex]——常数,默认设置值为0.09。
标准的[tex]k-\epsilon[/tex]模型,是针对湍流发展非常充分的湍流流动来建立的,也就是说,它是一种针对高Re数的湍流计算模型,而当Re数比较低时,比如在近壁区域内的流动,湍流发展并不充分,湍流的脉动影响可能不如分子粘性的影响大,在更贴近壁面的底层内,流动可能处于层流状态。因此,对Re数较低的流动使用此模型计算就需要对壁面进行处理,以解决近壁面区域内的流动计算及低Re数时的流动计算问题。常用的解决办法是采用壁面函数法。
流体近壁面可分为三个层:最里面一层称为”粘性子层“,流动几乎为层流,粘性是主要作用力;外面一层称为”充分湍流层“,湍流是主要作用力;它们之间有一个过渡层,粘性力和湍流的影响相当。本模型用标准壁面函数来模拟近壁面的流动。
动量:
[tex]U^{\ast}=\frac{1}{\kappa}\ln(E y^{\ast})[/tex] (4-28)
其中[tex]\kappa[/tex]——冯·卡门系数,等于0.4187。
[tex]E[/tex]——经验系数,等于9.793。
[tex]y^{\ast}=\frac{\rho C_{\mu}^{1/4} k_{p}^{1/2} y_{p}}{\mu}[/tex] (4-29)
其中[tex]k_{p}[/tex]——p点的湍动能
[tex]y_{p}[/tex]——p点离壁面的距离
当[tex]30\le y^{\ast} \le 300[/tex]时,标准壁面函数是正确的。在Fluent中,应在[tex]y^{\ast} \ge 11.225[/tex]时应用。当[tex]y^{\ast} \le11.225[/tex]时,则[tex]U^{\ast}=y^{\ast}[/tex]。
能量:
[tex]T^{\ast}=\frac{(T_{w}-T_{p})\rho c_{p} C_{\mu}^{1/4} k_{p}^{1/2}}{q}[/tex] (4-30)
其中[tex]T_{w}[/tex]——壁面温度
[tex]T_{p}[/tex]——p点温度
至此,模型的建立和计算前的设置均已经完成。
第三章 物理模型的建立
为了模拟板翅式换热器的换热和流动特性,首先设计一台空气——空气板翅式换热器,以作为数值模拟的模型基础和参考。
3.1 原始数据
表3-1 原始数据
热空气 冷空气
入口温度[tex]^{\circ}C[/tex] 180 40
入口压力[tex]MPa[/tex] 0.2648 0.1013
入口质量流量[tex]kg/h[/tex] 3200 5600
换热器效率 [tex]\ge 0.75[/tex]
压降[tex]MPa[/tex] [tex]\le 0.4[/tex] [tex]\le 1[/tex]
流动长度[tex]mm[/tex] 480 270
3.2 平均温度及物性参数计算
首先假设换热器的效率为75%,则:
[tex]\because \quad W_{1}=W_{min}[/tex]
[tex]\therefore \quad \eta=\frac{t_{1}^{'}-t_{1}^{''}}{t_{1}^{'}-t_{2}^{''}}[/tex]
[tex]t_{1}^{''}=t_{1}^{'}-\eta(t_{1}^{'}-t_{2}^{''})=180-0.75\times(180-40)=75^{\circ}C[/tex]
[tex]\because \quad \eta=\frac{W_{2}(t_{2}^{''}-t_{2}^{'})}{W_{1}(t_{1}^{'}-t_{2}^{'})}[/tex]
[tex]\therefore \quad t_{2}^{''}=\eta\frac{W_{2}}{W_{1}}(t_{1}^{'}-t_{2}^{'})+t_{2}^{'}[/tex]
假设[tex]c_{p1}=c_{p2}[/tex],则:
[tex]t_{2}^{''}=0.75\times \frac{3200}{5600}\times(180-40)+40=100^{\circ}C[/tex]
由于[tex]C^{\ast}=\frac{W_{min}}{W_{max}}=\frac{W_{1}}{W_{2}}\approx \frac{q_{m1}}{q_{m2}}=\frac{3200}{5600}=0.571\le 0.5[/tex]
取算术平均温度作为其平均温度:
[tex]t_{m1}=\frac{t_{1}^{'}+t_{1}^{''}}{2}=\frac{180+75}{2}=127.5^{\circ}C[/tex]
[tex]t_{m2}=\frac{t_{2}^{'}+t_{2}^{''}}{2}=\frac{40+100}{2}=70^{\circ}C[/tex]
根据平均温度[tex]t_{m1}=127.5^{\circ}C \quad t_{m2}=70^{\circ}C[/tex],求冷热空气的物性参数。
[tex]\mu_{1}\!=\!1.50619\!\times\! 10^{-6}\!\times\! \frac{(t_{m1}+273)^{1.5}}{t_{m1}\!+\!395}\!=\!1.50619\!\times\! 10^{-6}\!\times\! \frac{(127.5+273)^{1.5}}{127.5+395}\!=\!23.105\!\times\! 10^{-6}Pa\!\cdot\!s[/tex]
同理[tex]\mu_{2}20.576\times 10^{-6}Pa\cdot s[/tex]
[tex]\lambda_{1}=2.456\times 10^{-4}\times(t_{m1}+273)^{0.823}=2.456\times 10^{-4}\times(127.5+273)^{0.823}=3.4054\times 10^{-2}[/tex]
同理[tex]\lambda_{2}=2.9976\times 10^{-2}W/(m^{2}\cdot K)[/tex]
[tex]c_{p1}\!=\!1003+0.02t_{m1}+4\times 10^{-4}t_{m1}^{2}\!=\!1012.05J/(kg \cdot K)\!=\!1.0120 KJ/(kg \cdot K)[/tex]
同理[tex]c_{p2}=1006.36J/(kg\cdot K)=1.0064KJ/(kg\cdot K)[/tex]
[tex]P_{r1}=\frac{\mu_{1}c_{p1}}{\lambda_{1}}=\frac{23.105\times 10^{-6}\times 1012.05}{3.4054\times 10^{-2}}=0.6867[/tex]
同理[tex]P_{r2}=0.6954[/tex]
表3-2 冷热空气的物性参数
参数 [tex]\mu \; Pa\cdot s[/tex] [tex]\lambda \; W/(m^{2}\cdot K)[/tex] [tex]c_{p} \; KJ/(kg\cdot K)[/tex] [tex]P_{r}[/tex]
热空气 [tex]23.105\times 10^{-6}[/tex] [tex]3.4054\times 10^{-2}[/tex] [tex]1.0120[/tex] [tex]0.6867[/tex]
冷空气 [tex]20.576\times 10^{-6}[/tex] [tex]2.9976\times10^{-2}[/tex] [tex]1.0064[/tex] [tex]0.6934[/tex]
3.3 结构参数的计算
表3-3 产品结构尺寸表
热侧 冷侧
型面 平直型 平直型
翅片节距[tex]s/mm[/tex] 2.0 2.1
板间距[tex]b/mm[/tex] 4.7 6.5
翅片层数[tex]N[/tex] 7 8
翅片厚度[tex]\delta_{f}/mm[/tex] 0.3 0.3
隔板厚度[tex]\delta_{p}/mm[/tex] 0.5
侧板厚度[tex]\delta_{s}/mm[/tex] 2
封条厚度[tex]b_{s}/mm[/tex] 6
换热器高度:
[tex]L_{3}=N_{1}(b_{1}+2\delta_{p})+N_{2}b_{2}+2\delta_{s}=7\times(4.7+2\times 0.5)+8\times 6.5+2\times 2=95.9 mm[/tex]
翅片高:
[tex]h_{1}=b_{1}-\delta_{f1}=4.7-0.3=4.4 mm[/tex]
[tex]h_{2}=b_{2}-\delta_{f2}=6.5-0.3=6.2 mm[/tex]
翅片宽:
[tex]w_{1}=s_{1}-\delta_{f1}=2.0-0.3=1.7 mm[/tex]
[tex]w_{2}=s_{2}-\delta_{f2}=2.1-0.3=1.8 mm[/tex]
水力直径:
[tex]d_{h1}=\frac{2w_{1}h_{1}}{w_{1}+h_{1}}=\frac{2\times 1.7\times 4.4}{1.7+4.4}=2.4525 mm[/tex]
[tex]d_{h2}=\frac{2w_{2}h_{2}}{w_{2}+h_{2}}=\frac{2\times 1.8 \times 6.2}{1.8+6.2}=2.79 mm[/tex]
翅片面积比:
[tex]\varphi_{1}=\frac{A_{f1}}{A_{1}}=\frac{2N_{1}h_{1}L_{1}L_{2}/s_{1}}{2N_{1}(h_{1}+w_{1})L_{1}L_{2}/s_{1}}=\frac{h_{1}}{h_{1}+w_{1}}=\frac{4.4}{4.4+1.7}=0.7213[/tex]
[tex]\varphi_{2}=\frac{A_{f2}}{A_{2}}=\frac{h_{2}}{h_{2}+w_{2}}=\frac{6.2}{6.2+1.8}[/tex]
传热面积密度:
[tex]\beta_{1}=\frac{A_{1}}{A_{p1}}=\frac{2N_{1}L_{1}L_{2}(h_{1}+w_{1})/s_{1}}{L_{1}L_{2}N_{1}b_{1}}=\frac{2(h_{1}+w_{1})}{b_{1}s_{1}}=\frac{2\times(4.4+1.7)}{4.7\times 2.0\times 10^{-3}}=1298 m^{2}/m^{3}[/tex]
[tex]\beta_{2}=\frac{A_{2}}{A_{p2}}=\frac{2(h_{2}+w_{2})}{b_{2}s_{2}}=\frac{2\times(6.2+1.8)}{6.5\times 2.1\times 10^{-3}}=1172 m^{2}/m^{3}[/tex]
空气流通面积:
[tex]A_{c1}=N_{1}{(L_{2}-1.5b_{s})b_{1}-[\frac{L_{2}-1.5b_{s}}{s_{1}}(s_{1}-\delta_{f1})+(\frac{L_{2}-1.5b_{s}}{s_{1}}-1)b_{1}]}=7\times{(270-1.5\times5)\times 4.7-[\frac{270-1.5\times 6}{2}\times(2-0.3)+(\frac{270-1.5\times 6}{2}-1)\times 4.7]}=2.7734\times 10^{-3}m^{2}[/tex]
[tex]A_{c2}=N_{2}{(L_{1}-2b_{s})b_{2}-[\frac{L_{1}-2b_{s}}{s_{2}}(s_{2}-\delta_{f2})+(\frac{L_{1}-2b_{s}}{s_{2}}-1)b_{2}]}=1.1923\times 10^{-3}m^{2}[/tex]
空气迎风面积:
[tex]A_{y1}=(L_{2}-1.5b_{s})(L_{3}-1.5\delta_{s})=(270-1.5\times 6)\times(95.9-1.5\times 2)\times 10^{-6}=0.024247m^{2}[/tex]
[tex]A_{y2}=(L_{1}-2b_{s})(L_{3}-2\delta_{s})=(480-2\times 6)\times(95.9-2\times 2)\times 10^{-6}=0.043009m^{2}[/tex]
孔度:
[tex]\sigma_{1}=\frac{A_{c1}}{A_{y1}}=\frac{2.7734\times 10^{-3}}{0.024247}=0.11441[/tex]
[tex]\sigma_{2}=\frac{A_{c2}}{A_{y2}}=\frac{1.1923\times 10^{-3}}{0.043009}=0.0277[/tex]
一次传热面积:
[tex]A_{p}=2N_{1}(L_{1}--1.5b_{s})(L_{2}-2b_{s})=2\times 7\times(480-1.5\times 6)\times(270-2\times 6)=1.701252[/tex]
二次传热面积:
[tex]A_{f1}=2N_{1}h_{1}L_{1}\frac{L_{2}-1.5b_{s}}{s_{1}}=2\times 7\times 4.4\times 480\times \frac{270-1.5\times 6}{2.0}=3.858624m^{2}[/tex]
[tex]A_{f2}=2N_{2}h_{2}L_{2}\frac{L_{1}-2b_{}s}{s_{2}}=2\times 8\times 6.2\times 270\times \frac{480-2\times 6}{2.1}=5.969006m^{2}[/tex]
3.4 传热计算
质量流量:
[tex]g_{m1}=\frac{q_{m1}}{A_{c1}}=\frac{0.889}{2.7734\times 10^{-3}}=320.545 kg/(m^{2}\cdot s)[/tex]
[tex]g_{m2}=\frac{q_{m2}}{A_{c2}}}=\frac{1.556}{1.1923\times 10^{-3}}=1305.041kg/(m^{2}\cdot s)[/tex]
雷诺数:
[tex]R_{e1}=\frac{g_{m1}d_{h1}}{\mu_{1}}=\frac{320.545\times 2.4525\times 10^{-3}}{23.105\times 10^{-6}}=34024.54[/tex]
[tex]R_{e2}=\frac{g_{m2}d_{h2}}{\mu_{2}}=\frac{1305.041\times 2.79\times 10^{-3}}{20.576\times 10^{-6}}=176956.86[/tex]
由雷诺数可知,流体处于充分发展的湍流状态,采用Gnielinsk公式:
[tex]f_{1}=(1.58\lnR_{e1}-3.28)^{-2}\!=\!(1.58\ln(34024.54)-3.28)^{-2}\!=\!6.532842\times10^{-3}[/tex]
[tex]f_{2}\!=\!(1.58\ln R_{e2}-3,28)^{-2}\!=\!(1.58\ln(176956.86)-3.28)^{-2}\!=\!3.999600\!\times\!10^{-3}[/tex]
[tex]N_{u1}=\frac{(f_{1}/2)(R_{e1}-1000)P_{r1}}{1+12.7(f_{1}/2)^{0.5}(P_{r1}^{2/3}-1))}=88.28[/tex]
[tex]N_{u2}=\frac{(f_{2}/2)(R_{e2}-1000)P_{r2}}{1+12.7(f_{2}/2)^{0.5}(P_{r2}^{2/3}-1))}=277.94[/tex]
[tex]\alpha_{1}=\frac{N_{u1}\lambda_{1}}{d_{h1}}=\frac{88.28\times 3.4054\times 10^{-2}}{2.4525\times 10^{-3}}=1225.82W/(m^{2}\cdot K)[/tex]
[tex]\alpha_{2}=\frac{N_{u2}\lambda_{2}}{d_{h2}}=\frac{277.94\times 2.9976\times 10^{-2}}{2.79\times 10^{-3}}=2986.21W/(m^{2}\cdot K)[/tex]
翅片参数:
[tex]m_{1}=\sqrt{\frac{2\alpha_{1}}{\lambda_{f1}\delta_{f1}}}=\sqrt{\frac{2\times 1225.82}{175\times 0.3\times 10^{-3}}}=216.10m^{-1}[/tex]
[tex]m_{2}=\sqrt{\frac{2\alpha_{2}}{\lambda_{f2}\delta_{f2}}}=\sqrt{\frac{2\times 2986.21}{175\times 0.3\times 10^{-3}}}=337.28m^{-1}[/tex]
[tex]m_{1}h_{1}=216.10\times4.4\times 10^{-3}=0.950828[/tex]
[tex]m_{2}h_{2}=337.28\times 6.2\times 10^{-3}=2.092236[/tex]
[tex]\eta_{f1}=\frac{tanh(m_{1}h_{1})}{m_{1}h_{1}}=\frac{tanh(0.950828)}{0.950828}=0.7784[/tex]
[tex]\eta_{f2}=\frac{tanh(m_{2}h_{2})}{m_{2}h_{2}}=\frac{tanh(2.091136)}{2.091136}=0.4638[/tex]
有效传热面积:
[tex]A_{ef1}=A_{p}+\eta_{f1}A_{f1}=1.701252+0.7784\times 3.858624=4.704940m^{2}[/tex]
[tex]A_{ef2}=A_{p}+\eta_{f2}A_{f2}=1.701252+0.4638\times 5.969006=4.469675m^{2}[/tex]
两侧总有效传热面积:
[tex]A_{1}=A_{p}+A_{f1}=1.701252+3.858624=5.559876m^{2}[/tex]
[tex]A_{2}=A_{p}+A_{f2}=1.701252+5.969006=7.670258m^{2}[/tex]
两侧表面效率:
[tex]\eta_{01}=1-\frac{A_{f1}}{A_{1}}(1-\eta_{f1})=1-\frac{3.858624}{5.559876}\times(1-0.7784)=0.846207[/tex]
[tex]\eta_{02}=1-\frac{A_{f2}}{A_{2}}(1-\eta_{f2})=1-\frac{5.969006}{7.670258}\times(1-0.4638)=0.582728[/tex]
壁面热阻:
[tex]R_{w}=\frac{\delta_{p}}{\lambda_{w}A_{p}}=\frac{0.5\times 10^{-3}}{175\times 1.701252}=1.679435\times 10^{-6}K/W[/tex]
忽略污垢热阻,则:
[tex]\frac{1}{KA}=\frac{1}{\eta_{01}\alpha_{1}A_{1}}+R_{w}+\frac{1}{\eta_{02}\alpha_{2}A_{2}}=2.4999\times 10^{-4}[/tex]
[tex]KA=4000.10W/K[/tex]
传热单元数:
[tex]NTU=\frac{KA}{W_{min}}=\frac{4000.1}{0.889\times 1.012\times 10^{3}}=4.4462[/tex]
德思克近似公式:
[tex]\eta_{i}=1-exp{\frac{NTU^{0.22}}{C^{\ast}}[exp(1-C^{\ast}NTU^{0.78})-1]}=0.7503[/tex]
[tex]\eta=\frac{(\frac{1-C^{\ast}\eta_{i}}{1-\eta_{i}})^{2}-1}{(\frac{1-C^{\ast}\eta_{i}}{1-\eta_{i}})^{2}-C^{\ast}}=0.9053[/tex]
换热器传热热流量:
[tex]\Phi=\eta W_{min}(t_{1}^{'}-t_{2}^{'})=0.9053\times 0.889\times 1.012\times 10^{3}\times(180-40)=114.03KW[/tex]
流体出口温度:
[tex]t_{1}^{''}=t_{1}^{'}-\frac{\Phi}{W_{1}}=180-\frac{114.03}{0.889\times 1.012\times 10^{3}}=53.253^{\circ}C[/tex]
[tex]t_{2}^{''}=t_{2}^{'}+\frac{\Phi}{W_{2}}=40+\frac{114.03}{1.556\times 1.0064\times 10^{3}}=112.818^{\circ}C[/tex]
与假设效率误差:
[tex]\Delta\eta=|\frac{\eta-\eta_{s}}{\eta_{s}}|=\frac{0.0003}{0.75}=20.71%[/tex]
3.5 阻力计算
热侧阻力:
[tex]v_{1}^{'}=\frac{RT_{1}^{'}}{p_{1}^{'}}=\frac{287\times(180+273)}{0.2648\times 10^{6}}=0.4910m^{3}/kg[/tex]
设[tex]\Delta p_{1}=10000Pa[/tex]:
[tex]v_{1}^{''}=\frac{RT_{1}^{''}}{p_{1}^{''}}=\frac{287\times(53.253+273)}{(0.2648-0.01)\times 10^{6}}=0.3675m^{3}/kg[/tex]
[tex]v_{m1}=\frac{v_{1}^{'}+v_{1}^{''}}{2}=\frac{0.4910+0.3675}{2}=0.4292 m^{3}/kg[/tex]
由[tex]\delta_{1}=0.1144[/tex],得[tex]\delta^{2}=0.0131[/tex],查图2-4得[tex]K_{1}^{'}=0.46\quad K_{1}^{''}=0.85[/tex]
[tex]1-\delta_{1}^{2}+K_{1}^{'}=1-0.0131+0.46=1.4469[/tex]
[tex]\frac{v_{1}^{''}}{v_{1}^{'}}=\frac{0.3675}{0.4910}=0.7485[/tex]
[tex]2(\frac{v_{1}^{''}}{v_{1}^{'}}-1)=-0.5031[/tex]
[tex]4f_{1}\frac{L_{1}}{d_{h1}}\cdot \frac{v_{m1}}{v_{1}^{'}}=4\times 6.532842\times 10^{-3}\times \frac{480\times 2}{2.4525}\times \frac{0.4292}{0.4910}=8.9413[/tex]
[tex](1-\delta_{1}^{2}-K^{''})\frac{v_{1}^{''}}{v_{1}^{'}}=(1-0.0131-0.85)\times 0.7485=0.1025[/tex]
设局部阻力损失系数为[tex]\xi_{a}=5[/tex],则局部损失为:
[tex]\xi_{a}\frac{v_{m1}}{v_{1}^{'}}=5\times \frac{0.4292}{0.4910}=4.3707[/tex]
[tex]\frac{g_{m1}^{2}v_{1}^{'}}{2}=\frac{320.545^{2}\times 0.4910}{2}=25224.9033[/tex]
[tex]\Delta p_{1}\!=\!\frac{g_{m1}^{2}v_{1}^{'}}{2}[(1-\delta_{1}^{2}+K_{1}^{'})+2(\frac{v_{1}^{''}}{v_{1}^{'}}-1)+4f_{1}\frac{L_{1}v_{m1}}{d_{h1}v_{1}^{'}}-(1-\selta_{1}^{2}-K_{1}^{''})\frac{v_{1}^{''}}{v_{1}^{'}}+\xi_{a}\frac{v_{m1}}{v_{1}^{'}}]=3.570156\times 10^{5}[/tex]
压降符合设计要求。冷侧预设[tex]\Delta p_{2}=25300Pa[/tex],采用与热侧相同的计算方式可得[tex]\Delta p_{2}=9.130742\times 10^{5}Pa[/tex],也符合设计要求。