5.1 模型计算调整

        模型在上一章的设置后，基本可以进行迭代求解了。只是在迭代之前，还需对影响收敛的一些参数进行调整，以加速收敛的速度。

        在控制方程以给定的方法离散化后，还必须对离散方程进行某种调整，并且对各未知量（速度、压力、温度）的求解顺序以及方式进行特殊处理。这些需要依赖流场计算方法（SIMPLE和SIMPLEC）来进行调整。

        SIMPLE是英文Semi-Implicit Method for Pressure-Linked Equation的缩写，意为”求解压力耦合方程组的半隐式方法“。SIMPLE算法的基本思想可描述如下：对于给定的压力场（它可以是假定的，或是上次迭代计算所得的结果），求解离散形式的动量方程，得出速度场。因为压力场是假定的或不精确的，这样，由此得到的速度场一般不满足连续方程。因此，必须对给定的压力场加以修正。修正的原则是：与修正后的压力场相对应的速度场能满足这一迭代层次上的连续方程。据此原则，我们把由动量方程的离散形式所规定的压力与速度的关系代入连续方程的离散形式，从而得到压力修正方程，由压力修正方程得出压力修正值。接着，根据修正后的压力场，求得新的速度场。然后检查速度场是否收敛。若不收敛，用修正后的压力值作为给定的压力场，开始下一层的计算，如此反复，直到获得收敛的解。

        SIMPLEC是SIMPLE的改进算法之一，由Van Doormal和Raithby提出。其稳定性较好，在计算中可以将亚松驰因子适当放大，特别是在层流计算时，如果没有在计算中使用辐射模型等辅助方程，用SIMPLEC可以大大加速计算速度。因此，本模型在层流计算时选用SIMPLEC算法，在湍流时选用SIMPLE算法。

        因为Fluent中解的方程为非线性，所以有必要对变量[tex]\phi[/tex]的变化进行控制。通常的方法便是调整亚松驰因子，以减小在迭代过程中[tex]\phi[/tex]的变化。一般情况下，一个单元（cell）中的新值[tex]\phi[/tex]依赖于上一个旧值[tex]\phi_{old}[/tex]。亚松驰因子[tex]\alpha[/tex]因此定义为：

[tex]\phi=\phi_{old}+\alpha \Delta \phi[/tex]        (5-1)

        由此公式可见，调节亚松驰因子直接影响着计算收敛的速度。在计算过程中，先以默认亚松驰因子迭代，当残差曲线下降过于缓慢时可适当减小亚松驰因子以加速收敛速度。

        初始化时迭代计算前最重要的一步，初始化数值是否恰当是影响计算收敛的最重要因素之一。本模型经过不断的摸索尝试，总结出恰当的初始化方式和数值。全局初始化以压力出口为参考，压力值设为1000Pa。待全局初始化完毕，再对其进行适当的修改。在Path面板中，设置Fluid zone的压力为1000Pa，Z方向的速度值为速度入口的值，温度为300K。

        收敛条件以默认值为准，即残差值分别为：Continuity 1e-3；X-Velocity 1e-3；Y-Velocity 1e-3；Z-Velocity 1e-3；k 1e-3；epsilon  1e-3；Energy 1e-6。绘制残差曲线以监视计算收敛情况。

        另外，在进行迭代计算前还需建立等值面（ISO-Surface）用以生成等值线图和矢量图。以[tex]y=3mm[/tex]建立Surface Zone，即板翅式换热器模型在其高度一半处沿流动方向的一个分割面。

        计算残差图如下：

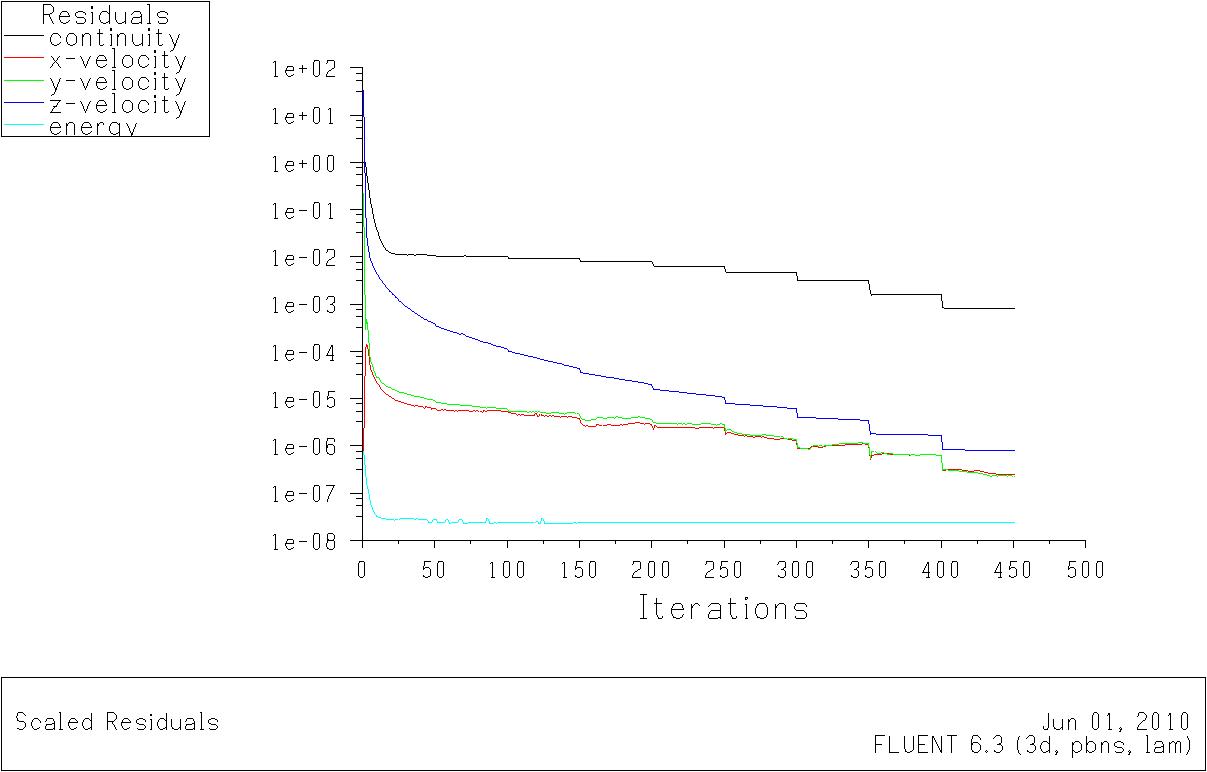
图 5-1 模型一在Re=500时的残差图

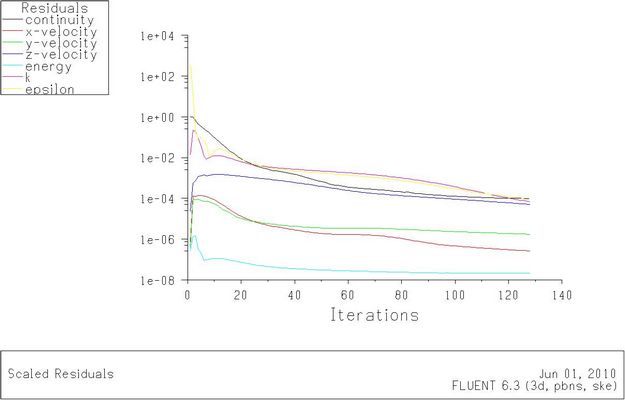
图 5-2 模型一在Re=9500时的残差图

5.2 计算结果分析

5.2.1 换热分析

        当流体从空间进入管道时，流动的边界层会有一个从零到汇合于流道中心线的过程。相同的，热边界层也如此。当热边界层汇合于中心线后，换热已经充分发展，此后的换热强度将不再保持不变。如图5-3所示。

图5-3（a）Re=500时温度分布图

图5-3（b）Re=9500时温度分布

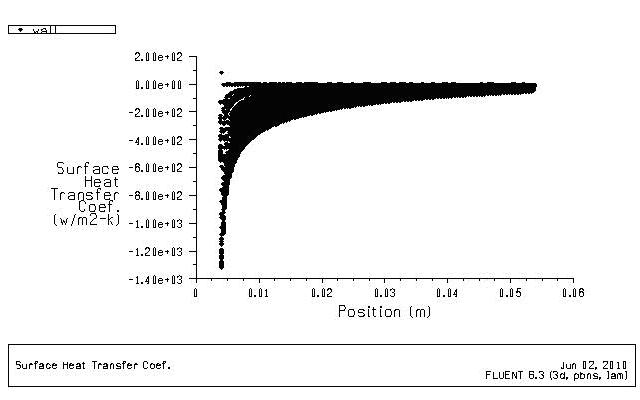
        入口段的热边界层较薄，局部换热系数比充分发展段的高，且沿流动方向逐渐降低。如图5-4 可以反映这点。

图 5-4 局部换热系数沿流动方向的变化

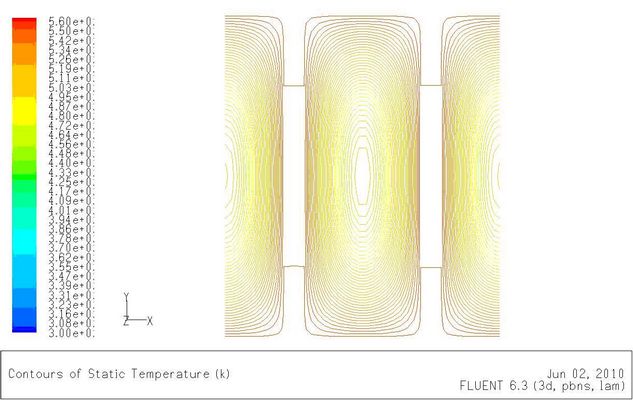
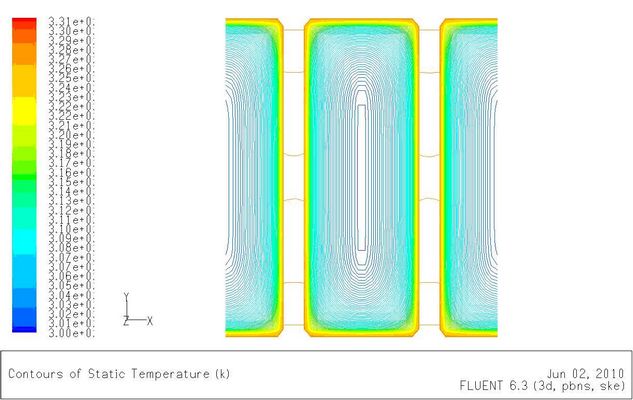
        流体在热边界层内的换热剧烈，温度从壁面到热边界层外迅速降低。此后，温度与流体的主流温度变化微小，近似呈恒温状。平直型的板翅式换热器，其流道相当于圆管。热边界层的发展也类似于圆管。图5-5（a）是Re=500时垂直于流动方向40毫米处截面的温度分布，图5-5（b）是Re=9500时垂直于流动方向40毫米处处截面的温度分布。比较两图可以发现在高雷诺数时热边界层发展较快，在相同距离处其厚度较低雷诺数要大。因此可以推断，平直型的板翅式换热器在高雷诺数时其换热性能低于低雷诺数。

图 5-5（a）Re=500时，40毫米处温度分布

图5-5（b）Re=9500时，40毫米处温度分布

5.2.2 阻力分析

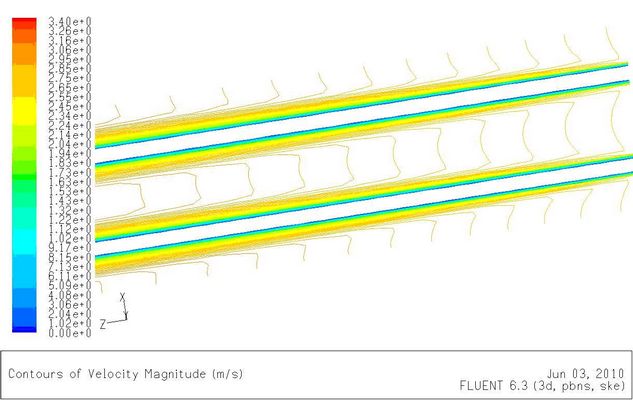
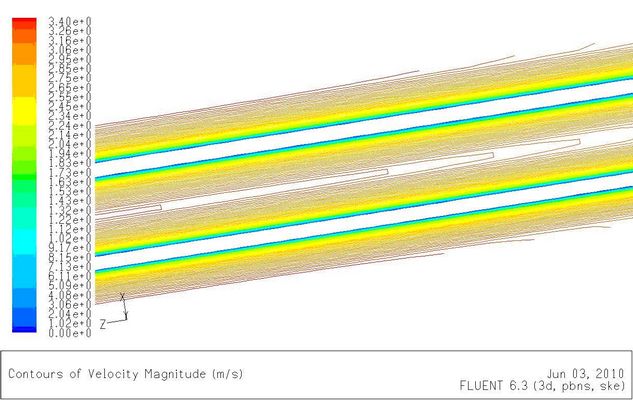
        如图5-6（a），在z=0处开始，流体在壁面上被滞止，形成边界层。边界层外即流道中心，仍保持较为均匀的流速，为核心流。由壁面不滑移条件引起壁面附近的流速降低，为满足质量守恒定律，核心流流速增大，速度等值线由平坦逐渐变为凸出。随着边界层厚度不断增长，核心流不断加速，直至四周边界层相遇，如图5-6（b）。整个流道被边界层流动充满，此后速度等值线不再变化。

图5-6（a）入口处速度分布

图5-6（b）流道中段速度分布图

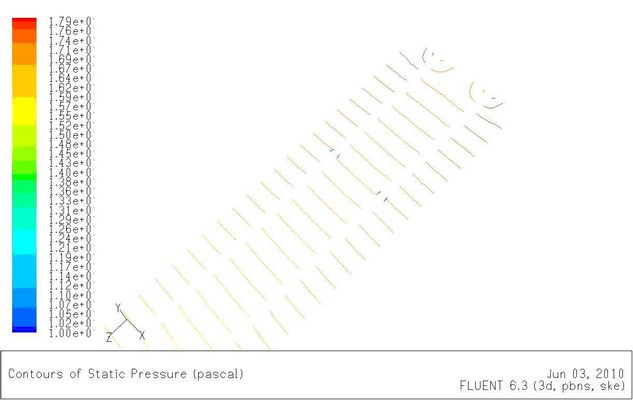
    观察图5-7入口处压力等值线，可以发现在流道入口处存在较大压降。此处的压降可以解释为两点：一是如图5-6（a）所示，是由于均流加速成充分发展流动引起的压降；二是入口段壁面速度等值线陡峭，壁面切应力大于充分发展段的壁面切应力，为克服这不负阻力差值所需要的压降。

图5-7入口压力分布图

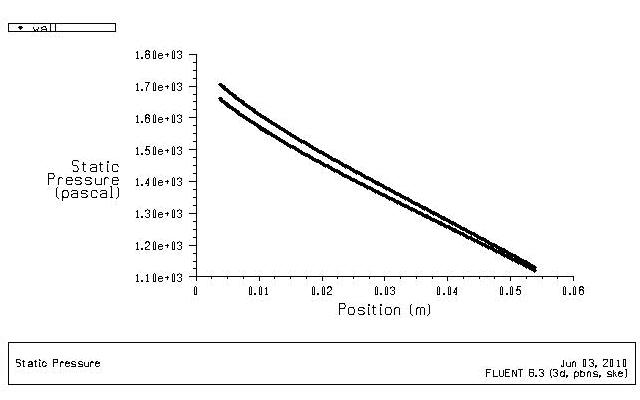
        观察图5-8摩擦因子沿流动方向的数值变化，在入口处由于入口效应的影响其摩擦因子较大。随后其数值逐渐降低，是由于随着流体向充分流动的发展，流体趋于稳定。但随后摩擦因子略微增加，是因为随着流速的增加流体的粘性底层逐渐变薄，流动由“水力光滑区”向“粗糙区”发展。管壁的粗糙度影响逐渐显现，摩擦因子增大。平直型翅片的压强降落平滑，压降数值不高，如图5-9. 

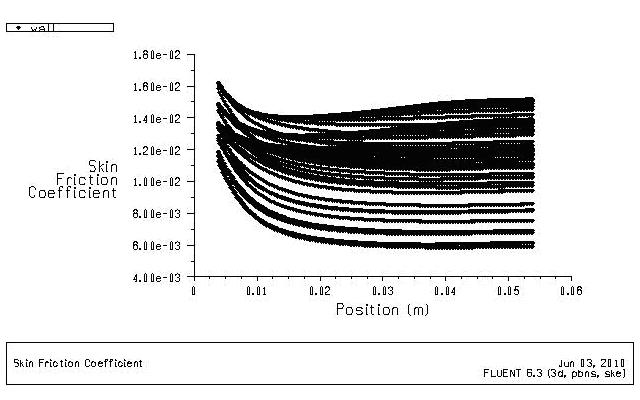
图5-8 摩擦因子沿流动方向的数值分布

图5-9压强沿流动方向的降落

5.2.3  j,f因子综合分析

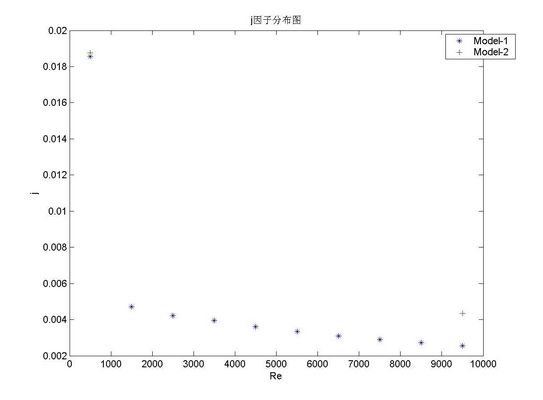
         由j因子分布图可知，平直型翅片在高雷诺数时换热效率差，所以其应该用于低雷诺数的范畴。相同雷诺数下模型二j因子与模型型一的比较可以看出，翅片高度对j因子的影响。在较高的翅片高度时，其换热效率较高。但由于翅片属于二次表面，其传热效率低于一次传热表面，所以可以预见在更大的翅片高度时相同雷诺数下其j因子反而会减小。这是由翅片的特性决定的。

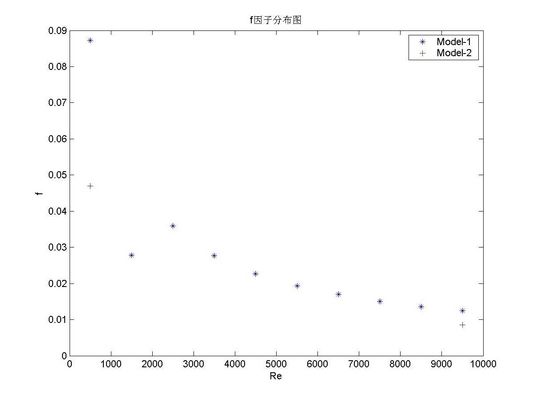
         由f因子的分布图可知，平直型翅片是一种适合应用于较低压降的翅片形式。如粘度较高的液体，或夹杂着固体颗粒的流体。这是由其简单的流道结构决定的。在相同雷诺数下模型二与模型一的对比可以看出，在较大的翅片高度下摩擦因子较小。这是因为模型二与模型一翅片宽度相近，在较大的翅片高下其最小自由流通面积较大，摩擦阻力减小。

图5-10 j因子分布图

图5-11 f因子分布图

        由于计算资源的限制，未能得到更多的模拟数据。但从现有的数据来看，猜测平直型翅片的j，f因子除与雷诺数相关外，还与翅片高度与宽度相关。但具体说来，应该是与翅片高与宽的比值有很大的关联。在某一雷诺数下，应该存在一个恰当的高宽比，使j，f因子达到最大，即整体效率最高。