在一个100条语句的列表中，第n条语句是“在这个列表中，恰有n个语句为假”

a）从这些语句中你可以得出什么结论？
b）若第n条语句是“在这个列表中，至少有n个语句为假”，回答问题a
c）假设这个列表包含99条语句，回答问题b

分析：

a）由题目可以得知，这100条语句中至多有1句是真的。

假设第1条语句为真

即：”在这个列表中，恰有1条语句为假“为真，那么在第2至100条语句中恰有一条为假，其它的为真。

考查第2句”在这个列表中，恰有2条语句为假“。若它是真的，那么和第1句矛盾，那么它是假的。

同理考查第3句”在这个列表中，恰有3条语句为假“。若它是真的，那么和第1句矛盾；若它是假的，也和第1句矛盾（因为第2句已经为假）。

所以，第1句是假的。

假设第2条语句为真

即：“在这个列表中，恰有2条语句为假”为真，那么在第3至100条语句中恰有一条为假，其他的为真。

推理过程同上，可发现第2句也是假的。

以此类推，让我们考查最后两条语句。

假设第99条语句为真

即：“在这个列表中，恰有99条语句为假”为真，第1至98句已经知道为假，那么考查第100句。

若第100句为真，那么与第99句矛盾。因此第100句为假。

所以，第99条语句为真，其余语句为假。

b）首先假设第n条语句为真

即：“在这个列表中，至少有n条语句是假的”为真，那么我们考查第n-1句。

假设第n-1句为假

即：“在这个列表中，至少有n-1条语句为假”可以表述为“在这个列表中，至多有n-2条语句为假”。与假设第n条语句为真矛盾，所以第n-1条语句为真。

类推，0至n-1条语句都是真的。

从以上的推理中可以发现，在这个列表中若第n句为真，可以推断前面的语句都为真但并不能判断n+1句及其以后的真假。

但可以从这个性质可以推断出，如果这个列表是有限的，它不可能全部为真，所以在这个列表中有一个界限。

即假设第n句是最后一句真的，那么剩下的语句都是假的。所以：

假设第n句是最后一句真的，则：“在这个列表中，至少有n条语句为假”，可得不等式。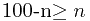

那么第n+1句：“在这个列表中，至少有n+1条语句为假”为假，可得不等式 。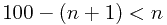

所以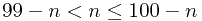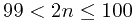：, 得 n=50 。

c）用第二题的方法来进行解答，即假设第n句为最后一句真语句。

则可得不等式：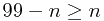

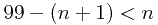
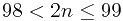
解的：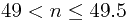                  

这种情况不会出现，这是一个悖论，并不是一个命题。

感谢kuoo和epegasus    bbs.chinaunix.net/viewthread.php